Soal dan Kunci Jawaban Konsep Bangun Ruang Kelas 5 Semester 2

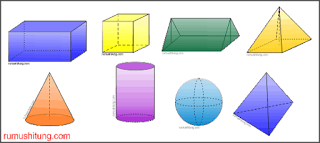
Sumber Foto: http://rumushitung.com/2013/06/18/koleksi-gambar-bangun-ruang-vector-cdr/

Konsep bangun ruang memiliki beberapa pengertian. Berikut ini akan dijelaskan konsep bangun ruang menurut Pamungkas, Negoro dan menurut penulis sendiri. Menurut Pamungkas (2012) bangun ruang merupakan bangun matematika yang memiliki isi atau volume. Bangun ruang dalam matematika dibagi menjadi beberapa bangun ruang yakni sisi, rusuk, dan titik sudut. Pada  Sisi merupakan bidang pada bangun ruang yang membatasi antara bangun ruang dengan ruangan disekitarnya. Rusuk merupakan pertemuan dua sisiyang berupa ruas garis pada bangun ruang sedangkan titik sudut adalah titik dari hasil pertemuan rusuk yang berjumlah tiga atau lebih.

Sedangkan menurut Negoro (2001) Jika suatu bangun tidak seluruhnya terletak dalam bidang, maka bangun itu disebut bangun ruang. Bangun ruang dibentuk oleh daerah segi banyak yang disebut sisi. Ada bermacam-macam bangun ruang, diantarnya prisma, kerucut, limas, kubus, tabung dan bola.

Bangun-bangun geometri baik dalam bangun ruang maupun bangun datar merupakan sebuah konsep abstrak. Artinya bangun-bangun tersebut bukan merupakan sebuah benda konkret yang dapat dilihat maupun dipegang. Bangun-bangun tersebut merupakan suatu sifat dari benda-benda konkret.

Disekolah dasar siswa kelas awal sudah harus dikenalkan konsep bangun ruang. Hal ini diperlukan untuk melatih daya titik ruang para siswa. Bangun-bangun yang dikenalkan di kelas awal merupakan bangun-bangun sederhana seperti kubus, balok, tabung, kerucut, limas, prisma dan bola.Untuk memvisualisasi konsep-konsep tersebut pada kelas awal tidak cukup bila hanya digambarkan di papan tulis. Guru harus memiliki alat peraga. Dari uraian di atas maka bangun ruang dapat didefinisikan sebagai bangun yang memiliki ruang, sisi, titik sudut dan rusuk.

Untuk soal-soal bangun ruang kelas 5 semester 2 dapat anda download di bawah ini

Sumber:

Negoro, S., & Harahap, B. (2001). Ensiklopedia Matematika. Jakarta: Ghalia Indonesia.

Pamungkas , A. (2012, April 11). Diwarta. Dipetik April 2012, 2012, dari Diwarta Web site: http://www.diwarta.com